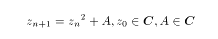
フラクタルというのは自己相似性を有し、かつ無限に細かく複雑な構造を持った図形のことです。さまざまな種類のものがあり、どれも面白い形をしたものばかりです。有名なものにマンデルブロート集合やジュリア集合などがあります。自らプログラムを書いて描いてみたことのある方もいらっしゃると思います。
フラクタル図形は平面図形(2D)として描かれることが多いのですが、今回は何種類かの3Dのフラクタル図形をPC-9821上で描くプログラムを製作しました。3Dにすることによって計算量、使用メモリともに莫大なものになるので、全てアセンブリ言語で書いた上で、特殊な方法によりリアルモードからプロテクトメモリを直接利用しています。
紙面の都合により今回扱っている図形を全て紹介することはできませんが、そのうちの1部の図形について説明をしたいと思います。
1つ目は、1つの正4面体の各面に、新たに辺の長さが半分の正4面体を付け加え、さらにその半分の辺の長さの正4面体を各面に付け加え…という操作を無限に繰り返して得られる図形です。これはいわゆる再帰図形と呼ばれるもので、2Dではコッホ曲線が有名です。
フラクタルとして十分に許される程度まで細かく正4面体を付け加えて行くと、最終的に描く正4面体の数は大体1000万個程度(実際にはプログラムの都合によりもっと増える)という膨大な数になります。そのため、全てアセンブリ言語で書いてPentium上で動作させていながら、なお描画速度には難があります。
2つ目の図形は、簡単にいうとジュリア集合の3D版です。2Dのジュリア集合の描画については、漸化式
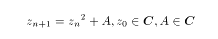
についてAの値を固定し、複素平面上でZ0を動かし、Znの収束発散をみて、それに対応した色の点をうつという方法が一般的ですが、ここでAを固定せずにZ0と合わせて動かすと複素数の変数が二つとなり、4次元空間におけるフラクタルとなります。その4次元空間から適当に3次元の空間を切りとって表示すればめでたく3Dフラクタルとなるわけです。
当たり前のことですが、そのまま点を塗りつぶすと空間が埋めつくされて何が表示されているのか分からなくなってしまうので、透過処理などを施しています。
まあ、こうした理論はともかく、百聞は一見にしかずということでとにかく見てみて下さい。フラクタル図形の美しさを満喫して頂けると思います。