
はじめに
オリパンフ号の「PCM への誘い」よりはや8ヶ月。皆様いかがお過ごしでしょうか。
理論科学してますか?(笑)>>一年生
今回は、ここのところ私がどっぷりはまっていた MPEG-Audio のお話です。
序章
画像では JPEG というフォーマットが有名ですね。絵を細切れに分割して、それぞれに対して周波数領域で効果的にデータを捨てることによって圧縮を行うものです。非可逆ではありますが、高い品質と圧縮率を誇っています。符号理論的な圧縮方法では全然縮まないフルカラーの絵に対する決定版とも言える方法ですね。
一方、音声圧縮に目を向けると、長い間線形予測を基本とした圧縮方法が主流でした。ADPCM(Adaptive Differation PCM)(*)、CELP(Code Exited Linear Prediction)などですね。これらはみな、電話音声の送信のために開発されています。そのためデータ量は非常に小さいのですが、いかんせん音質がよくありません。
(*)G.721 とかのことです。X86K や OPNA に載ってたものや、IMA 規格、MS-ADPCM みたいなのも略は同じADPCM ですが、あんな Toy program みたいなちゃちなものではありません:)
なぜ音声では JPEG のようなことがなかなかやられてこなかったのでしょう?時間で分割し DCT などを使って非可逆圧縮を施してやれば、高音質のデータもかなり圧縮できそうだと思うのは人情というものです。
「PCM への誘い」でも書きましたが、人間は周波数成分で音を聞いています。もう少し詳しく言えば、三半器官が共鳴管の役割をしていて、共振する位置を感じて音を聞いているわけです。ここで時間領域で音に一瞬の段差を入れてみます。すると、段差のある信号のスペクトル解析をしたことがある人はイメージしやすいと思いますが、一瞬のノイズが聞こえるのではなくてその前後(*)の音ごと乱されます。このため、JPEGのように段差ができたのでは、「ちょっとブロックノイズが目立つかねえ。がははは」と笑って済ますわけにはいかないのです:)しかも人間の聴覚の感度は最もいい所で120dB(**)くらいあります。これでは、おいそれと時間で分割していじってしまうわけにいかないのも無理はありません。
(*)前と聞くと「おや?」と思うかもしれませんが、周波数成分で聞くと言うことは必ず遅延があるということなのです。
(**)約20bit
周波数帯域分割
だからといって、方法がないわけではありません。こんなところで弱音を吐いては工学者失格ですね(笑)
まずは原始的に考えましょう。つなぎ目に段差ができてまずいなら、つなぎ目を目立たなくすればいいわけです。例えば、DCT のつなぎ目が互い違いに来るように2系統データを作っておき、片方がつなぎ目に来る時はもう一方のデータの比率が高くなるように滑らかに合成するという方法が思い付きます。滑らかさが足りなければ3系統、4系統と増やせばいいわけです。
ですが、冷静に考えると上の方法はかなりお馬鹿さんです(^^; 圧縮しようと思ったのに2倍、3倍のデータを持たなくちゃいけないんでは、元も子もないでしょう。とはいえ、データ量を変えずに何系統にもデータを分割するには、一体どうしたらいいのでしょう?
タイトルに見えちゃってるのがご愛敬ですが、答えは周波数帯域分割です。
ここで、「PCM への誘い」で紹介した標本化定理を思い出してください。
「0 〜 f の周波数成分のみを含む信号は、サンプリング周波数 2f の標本点で一意に決まる」
これが、何故 0 〜 f だったかを思い出すと、これはそれ以外の周波数の音が映りこんできてしまうからでした。ということは、範囲外の周波数が含まれていないことさえ分かれば、別に f 〜 2f でも 2f 〜 3f でも構わないわけです。これで何が言いたいかというと、データを周波数成分の帯域別で n 個に分割すれば、それぞれの帯域は 1/n のデータで表せるわけです。これで、データ量を変えずにデータを分けることができます。あとは、がんがん分割数を多くしていけば、つなぎ目なんかどうってこと無くなってしまいます。やったぁ:D
多相フィルタバンク
しかし、世の中そんなに甘くはありません(^^;
電々の授業や実験で信号処理をやったことがある人なら想像がつくと思いますが、1/n の領域をきれいに取り出すバンドパス・フィルタなんて、アナログでもすごく大変だし、デジタルではそれこそ逆立ちして血の涙が出るくらい大変です(笑)それがあなた、n 個ですよ。そりゃあもう、この世の終わりってもんです(ぉ
というわけで、帯域フィルタ群なんて実用にならんよなあってな感じだったのですが、ここにきてプロセッサが速くなってきて、俄然日の目を見てきました。とはいってもまともに立ち向かってできるほど速くなったわけではありません(*)が、世の中には頭のいい人もいるもので、帯域間で折り返し成分をキャンセルさせて、一発で全部の帯域を計算する方法が開発されました。(**)それが多相フィルタバンクです。MPEG-Audio では 32 バンド 16 サンプル (計512サンプル)のフィルタバンクが用いられています。係数ベクタは規格で与えられているので、数学屋さんに感謝しつつ、ありがたく使わせてもらいましょう(^^;
(*)お金かけてもいいなら、DSP n 個でできますけどね:)
(**)私の専門は音声ではないので詳しくは知りません(笑) しかし、こういう難しいことをやんなきゃいけないんじゃ、音声の研究室に行った人は大変だねぇ(ぉ
ちなみに、MPEG-Audio の LayerIII や DOLBY AC3 では、フィルタバンクとDCT を合体させた MDCT (Modified Cosine Transform) で、一発で 512 個計算するらしいです(*)。MDCT は、数学的には多相フィルタバンク + DCT と同じなんだそうです。
(*)規格書は持ってるんですが、まだ読んでないので詳しくは知りません(笑
IDCT の高速化
さて、MPEG-Audio LayerI,II のデコードでは IDCT の結果をフィルタバンクにちびちび突っ込んでいくことになります。多相フィルタバンクの方は殆ど高速化は不可能なので、こいつくらいは頑張って高速化しましょう。
で、やらなきゃいけない変換は本質的には下の通りです。{i : 0 〜 31}

C(n) = cos(n×π/64) と置くと、(以下、C の () は適宜省略します)
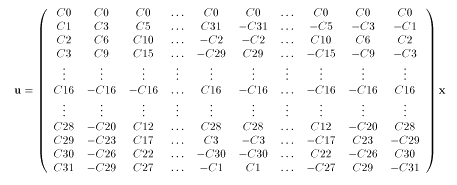
こうなります(でかい(^^;)。この行列では、n < 0, 32 <= n の範囲の要素は C(n) (0 <= n < 32) を使って表してあります。
見て気付くのは、上から順に 0 から番号をつけて、偶数の行は真ん中で左右対称、奇数の行は左右対称+符号反転で並んでいるということです。まあ、(2i+1)×π/64 は 0 〜 π まで回っていることを考えれば、偶数の行は整数周期入っていて奇数の列には+半周期入っているので当たり前です(^^;
では、上の行列をぐりっと折り返すイメージで、変数の置き換えを行いましょう。新たに a[i] = x[i] + x[31 - i], b[i] = x[i] - x[31 - i] として、偶数の行と奇数の行を別々に計算することにします。とりあえずこれで掛け算は半分ですね:)
さて、さらにどうにかならないか考えましょう。新しい行列の係数は、上の行列の右半分か左半分を見れば自明なので書くのは省略します(^^;偶数の行の方の係数を見ると、先程と全く同じ方法で偶数の行と奇数の行に分けることができることが分かります。この後も、偶数の行を分離した方は簡単にもう一回「ひねり」を加えることができます。が、問題は偶数の行を分離する度に残される奇数の行の方です。こっちの係数を見ると、同じようにぱたぱたひねってやりたくても、同じ係数が出てきませんので出来そうもありません。
ここで、奇数の行をもう一度並べて、じっと睨んでみましょう。
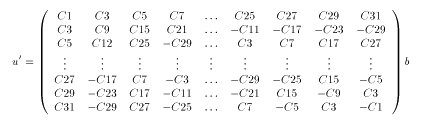
うーむ…
各行・列に同じ要素は一つもありません(^^; しかも、b の各要素に全種類の係数がかかっているようです。これでは一行は計算しないとどうしようもなさ そうです(;_;) しょうがないので、涙を飲んで計算することにします。しかし、ただで転んでは悔しいのでここから頑張りましょう。実際、ここからが根性の見せ所です(笑)
上の行列では、係数は奇数の16種類だけなっていますね…嫌な予感のしたあなた、多分正解です(^^;
ここで 2cosαcosβ = cos(α-β)+cos(α+β) を思い出してください。奇数の係数 C(2i+1) に、偶数の係数 2C(2j) をかけると C(2i+1-2j) + C(2i+1+2j) となり、どちらも奇数の係数になります。16種類の係数を細胞分裂(笑)させることができるわけです。これを使えば、1行だけ計算した後、それぞれに対して計4回の掛け算で、各 b の要素に対して係数を作ることができます。あとは、足し算引き算をうまくやって求める値を出しましょう:) この「うまくやる」というのがくせもので、実はすげー面倒なのですが、やることはできます。
え? ここでやれ?
じゃあ、まあ、ヒントということで最後に残される 2x2 の奴についてだけやりましょう(^^;
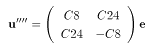
tmp00 = C(8) * e[0]; tmp01 = C(24) * e[1];
tmp10 = tmp00 + tmp01; tmp11 = 2 * C(16) * (tmp00 - tmp11);
u4[0] = tmp10;
u4[1] = tmp11 - tmp10;
はい。見事に掛け算が一個減りました(^^;
この調子で 4x4, 8x8, 16x16 も実装すれば出来上がりです(オイ
ちなみに、MADEC や MPAPLAY ではこの辺を gas でコプロ命令ぐりぐりいじって最適化してあるのですが、8x8 まではテンポラリの変数がコプロのレジスタに納まりました。16x16 では fld, fst の嵐なのですが、8x8 までは平和そのものです:) ハーフレート再生では 16x16 がいらないので、IDCT だけ見ると段違いに速くなってます:D
(おまけ☆)
上の例では係数を cos(nπ/64) でそのままぐいぐい押しましたが、実は 1/2×cos(nπ/64) に変換してから計算するとちょっといい事があります:)
実装に挑戦する人はトライしてみるといいでしょう。
終わりに
今回は MPEG-Audio をデコード側から眺めてみました。デコードも見るからに重そうですが、エンコードの方はもっと大変です(^^; 1024 点 FFT で周波数成分の分析を行い、各バンドのデータ量その他を決めたりとか、デコードには全くない処理も多くて泣きそうに重いです。ま、MAENC を使ったことのある人は身を以って体験したでしょうけど:)
蛇足ですが、MADEC/MAENC/MPAPLAY に対する要望、感想、苦情、ファンレター(笑)受付中ですのでよろしく☆:)
E-Mail: [email protected]
/ [email protected]
/ inu00002@いぬ。BBS (ぉ