DAT や CD 、MD の録音形式から電話回線、Windows の WAVE ファイルに MIDI 規格音源。一昔前まで、やれアナログだの FM 音源だの言ってたのものは、 ことごとく PCM 方式になってしまいました。
PCM とは一体何なのでしょう?
PCM とは「Pulse Code Modulation」の略で、音はアナログの連続量なのですが、 これを瞬時値(pulse)の離散的な連続に変換し、それぞれの瞬時値を デジタル(code)で表す変調*1 (modulation) だということです*2。
簡単に言えば、音の波形をやたらと沢山の数字の羅列で表すわけです。
何でこんなもんが流行っているかといえば、数字の羅列にするとコンピュータで 扱えるので、色々と便利なことがあるからです*3。
ま、これがTSGの部報に載ってる記事だと言うことからも明白ではありますが(笑)
ここまで聞いて、「そんな『変』調かけたら雑音が載るんじゃねーのか、 それに再生はどーすんだオイ」と思った人はいるでしょうか?
いたら、その人はかなり鋭い人です。鋭いけど、かなりの天邪鬼ですね(笑)
CDを聞いたりとか、「通話料が安くて音がいい」デジタルホンを使ったりとかした ことはないんでしょうか (^^;
別にいいですけど(笑)
実際問題として、色々な理論や技術に支えられて音を PCM として扱うことが できるようになったわけなのですが、画像と違って音は目で見て分かるわけでは ないし、アニメ絵のような扱いやすいデータを作ることもできないので、 PCM を扱うというのはかなり敷居の高い作業になってしまっています。
しかし、信号処理独特のものの見方に慣れれば、PCM のとても面白い世界が 見えてくるはずです。
本記事は「ほんのさわり」でしかありませんが、これをきっかけにあなたの プログラミングライフに「愉快な PCM (笑)」が加わることになれば 幸いです :)
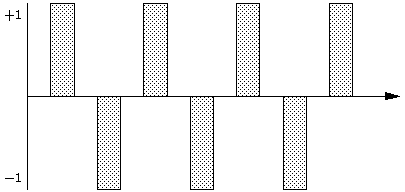
例として、瞬時値が 0 になった時点から 1 秒間に 8 千回の頻度でサンプリング する場合を考えてみます。
ここに 2kHz の正弦波を入れたらどうなるでしょう?

ですね。
では、6kHz の正弦波ではどうでしょう?
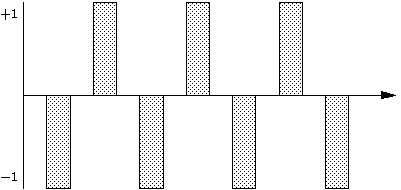
おや?
2kHz と同じ形になってしまいました。
よ〜く考えれば、これは単に
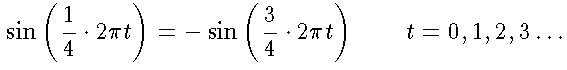
なだけなので、当たり前ですね (^_^;
同様に 1kHz, 7kHz, 9kHz... とか 3kHz, 5kHz, 11kHz... なども区別がつきません。
というわけで、詳しい説明は省きますが
という大定理があるわけです。
これを踏まえて、PCM 関連のデバイス、ソフトウェアは全て
ように作られています。
変調器には必ず高周波成分をカットするローパスフィルタが入っているし、 復調器は 0 〜 f の周波数成分のみを持つ信号を復元するように 色々と工夫がなされているわけです。
ちなみに、f より大きい周波数成分を周波数 2f でサンプリングすると 高周波成分は 0 〜 f に奇麗に折り畳まれてしまうので 「折り返し雑音」と呼ばれます。
さて、変復調のイメージもつかめた所でちょっと練習 :)
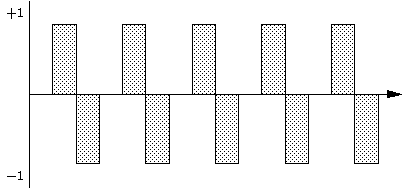
A-D 変換にも色々な技術があるのですが、ここではそれは置いといてうまいこと 離散量になったとして (^^;、そこから先の取り扱いについて考えてみます。
アナログ入力が -1 〜 +1 の時、これを Δ = 1/128 のきざみで離散量に 変換したとすると、うまく一番近い値が出力されていたと しても Δ/2 = 1/256 の誤差がでてしまいます。これを量子化誤差と言います。
一般的にデジタルの音が良いと言われるのは、デジタル回路を多少いい加減に 作っても、誤差を理論的に押さえ込む事ができるからです。アナログだと精度が 回路の出来や環境に左右されますからね :)
ま、デジタルでも電磁波とかα線*7 とかで誤動作する可能性はあるんですが(笑)
この原稿を読んでいる人には浮動小数点の扱いなどでお馴染みだと思うのですが、 コンピュータで離散量を扱う以上、量子化誤差や sin, log などの無限項必要な 計算の有限項での打ちきりによる誤差、似たような 信号の差での S/N 比*8 の悪化などは避けられません。
詳しい所は数値解析の教科書に譲りますが、PCM を扱うには誤差についての知識も 必要なわけです。
人間は一体、音をどういう風に知覚しているのでしょうか?
生理学的なことはよく知らないのですが、数十 Hz 〜 十数 kHz の 「周波数成分」を感じ取っているのだそうです。
CD のサンプリング周波数は 44.1kHz、DAT や MD は 48kHz なのですが、これは 可聴域の周波数成分を取り込むのに十分な速度であるわけです。
ところで「音の信号処理」と「音声処理」と言う言葉を聞いた事がありませんか?
これらの違いは一体何なのでしょう。
人間が声を出すというのは、「声道 (口) の形を変化させ、それにあわせて 音源 (声帯) を振動させて共鳴を起こし、空気中に指向性を持った音波を発射する」 行為で、その波形は 100 〜 300 Hz の特定波形の繰り返しになっています。
これを人間が感じる周波数成分から見てみれば、ある基本波とその高調波の 組み合わせパターンで音声が識別されていることが分かります。
「音声処理」というのは、発音されている音声に対しては短いけれども波形を 解析するには十分長い部分を切り出して、様々な波形を解析することをベースに行う 処理なのです。
一方、「音の信号処理」では音の遷移なども芸術性のうちなので、連続的な処理を 行います。とはいえ、部分的に切り出して波形の解析・操作を行う処理は 便利なので、うまく繋ぎ合わせて戻せるようにする研究も色々と行われています。
それから、「音の信号処理」では周波数成分によって位相の遅れ方の異なるような 処理は当然御法度になります*9。
というわけで、コンピュータで PCM データをいじっているとちょくちょく 出てくる処理として、サンプリング周波数のダウンコンバートについて 考えてみます。
まず、真正面から考えます。
周波数領域で作業するのだからフーリエ変換を行った後、低域成分だけで逆変換 してやればいいはずです。
しかし! 数十MBもあるような PCM データ全体に対してフーリエ変換を行うことは、 必要な精度、計算量とも悪夢のようなものであることは容易に想像がつきます。
細切れに処理して繋ぎ合わせる?
まあ、かなり難易度は高いでしょうができないことはないでしょう。
もっと簡単な処理でできないでしょうか?
幸い、PCM データを一定個数置きに間引くという処理に関しては、折り返し雑音 以外は入らないことが知られています。これを利用して何とかしましょう。
まず、元データのサンプリング周期単位でアナログ信号モデルを設定して 繋ぎ合わせたものを考えます。
ここでは、次のサンプル時刻まで値をホールドするモデルを考えましょう。
すると、考えたアナログ波形は直観的に
であることが分かります。
これより、アナログ波形のモデルから 変換先サンプリング周波数 xn (n は正整数) の周波数でサンプリングしたデータを作り高周波成分を 除去→間引き、という方針が成り立ちます。
ただし、このモデルに対してサンプリングの前処理としての高域除去はできないので、 n を十分大きくして折り返し成分を十分小さくします*11。 次に高周波成分の除去ですが、これはデジタルのローパスフィルタで 行います*12。
しかし間引きを行うためには、変換先サンプリング周波数/2 以下の成分は 殆ど完全に通し、それより大きい成分は殆ど完全に遮断しなくてはなりません。 それでいて遮断周波数が 1/n のフィルタというのは恐ろしく実現が難しいので、 ここでは2段階に分けてみます。
n を 4 の倍数*13 とし、初段では 4/n まで高域除去&間引きを行います。 こうすれば、初段のフィルタは 1/n 以下の低域を完全に通し、7/n 以上の高域は 完全に遮断する様なフィルタでさえあれば 1/n 以下の低域は 折り返し雑音に汚染されないわけです(笑)
で、次段では 1/4 の急峻なフィルタを気合を入れて作ります。
初段のフィルタでは入力信号は一定時間ホールドされているので、 係数を予めまとめておけば劇的に計算量が減ります。また、計算誤差も 小さくなります :)
次段も、間引き処理とセットになっているから出力に必要な項だけ 計算すればいいので、それ程計算量はいりません*14。
これだけ工夫すれば、Pentium クラスの CPU や DSP なら実時間の処理も 可能になりますね :)
しかし 5 章で紹介したように、信号処理の基礎程度のローテクでも 工夫次第では予想以上に良い結果が得られる事があったりします :)
PCM 関連ソフトウェアの実装では音質と計算時間のトレードオフがたまらなく 愉快です。是否一度 PCM 関連のツールを作ってみることをおすすめします。
大容量デバイス、高速な CPU、Windows、インターネット、CD で供給される ゲーム (^^; など、パソコンで PCM を扱う環境は急速に充実してきて いますしね☆
5 章ではいきなり怪しい内容になったような気がしますが、 気にしないことにしましょう (^^;
質問等がありましたら、メールをくれるなり、いぬ。に書き込むなり、 根津研に押しかけるなり(笑)してください。 僕に分かることなら何でもOKですので :->
[総目次へ]
[email protected]